2025年2月9日、2025年度(令和7年度)高専の入試が行われました。宮城県には仙台高専(旧電波高専および旧宮城高専)があります。船岡からだと東北本線で槻木、岩沼、館腰、名取と行けば宮城高専(名取高専とも呼ばれ、正式名称は仙台高専名取キャンパス)が通学しやすそうなので需要が高いと思われます。
なお、入試問題は日本全国の各都道府県にある他の高専と全く同じようです。ただし、宮城県のみ、どういうわけか数学の配転のみを2倍とする傾斜配点が行われていますので、数学で失点があると不利になります。逆に言うと数学で高得点であれば他の科目で多少失点があってもあまり問題にはなりません。また、なぜか大問4がプログラミング言語を意識していたので、プログラミングをやったことがある人は有利になるかと思います。
問題と解答そのものは高専の公式サイトにありますが、解説はないので作ってみました。
大問1
(1) 単なる計算
(2) 2つの連立方程式と言っていますが、4つの式で解が共通です。
なのでaもbもない2つの式から x=2 y=2 が分かればそれを代入します。
(3)2次関数の変化の割合は公立高校入試で40年ぐらい毎年出ていますが、反比例の変化の割合とは目新しいです。
普通に計算してもよいですが、反比例グラフでpからqまでの変化の割合
$$ – {a \over pq} $$
に代入すると楽です。
(4) 中学校では習わないはずの3次関数が出てきて度肝をやられます。
ただ、単なる定義域と値域の問題なので引っ掛からなければよいでしょう。
(5) ルートが整数になるということは、何かの2乗になるから、a=bの場合だから36通り中6通りと短絡的に考えてしまいますが、a=1かつb=4(と、その反対)でも4になります。一応図を描いてみると36通り中8通りでした。
また、相加平均と相乗平均が同じ場合というこれまた中学校では習わないはずの概念が出てきますが、これは間違いなくa=bの場合なので36通り中6通りです。
(6)本当はこういうのはそれこそPythonとかのプログラミング言語でやるべきですが、仕方ないので1個1個数値を小さい順に並べると一番多いのが3、平均は5.1です。
(7)てっきり中点連結定理の問題かと思ったらそうではなく、例えば点Qから頂点Aに補助線を引き、他の点も同様に補助線を引くと
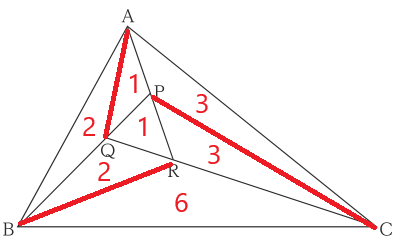
面積の大きさが何平方センチメートルとかは分からなくても、真ん中にある△PQRを基準にした時の比率なら分かります。数字を全部足すと18です。
(8) 実はこれ分かりませんでした。卑怯な手段ですがマークシート形式なので、答えは1~9のどれかしかありません。
で、三角錐なので答えが整数なら2でも3でも割り切れる数である6の倍数が絶対どこかにあるはずです。
図を見る限り三角錐の底辺の3角形の部分は二等辺三角形であり、三角錐の高さはその二等辺三角形の斜辺ではないところの2倍です。
高さは分からなくとも高さの斜辺は
$$ {9 \over 2} \sqrt{2} ≒ {9 \over 2} × 1.4 ≒ 6.1 $$
なので、図を見ると高さはそれより少し短いので6ぐらい?ひょっとしたら5かも?
とりあえず6の倍数なので高さを6として話を進めると、三角錐の底辺の三角形の斜辺ではないところの長さが3であり結果が9になりました。
模範解答を見たら当たってはいましたが、これはそもそもマークシート方式だからできたことであって、本来は計算で高さあるいは三角錐の底辺の三角形の斜辺ではないところの長さのどっちかを求める必要はあります。
大問2 またも反比例の問題です。高校入試問題では軽く流されるはずの反比例がやたら存在感を放っています。
(1) x=6と 分かっているので代入するだけ
(2) x座標は6より大きく1桁という時点で7~9のどれかしかありません。
かつ18を割り切れるのは1つしかありません。
(3) 2点の座標が分かるので
点A: 3 = 6a + b
点B: 2 = 9a + b
の連立方程式です。
(4) またもや中学校では絶対に習わないヘロンの公式を使うのかと思いましたが、△ABCをすっぽり覆うような長方形を描き(面積65/3)、そこから左上(面積50/6)、右上(面積3/2)、右下(面積35/6)にある3つの三角形の面積を引けば時間はかかりますが難しい知識は必要ありません。
大問3 図形の問題ですが、ラストは明らかに中学校で習わない内容でした。
(1) 弧の比率2:1というのが分かりにくいですが、要は弧AQは円周を6分の1に分けているので中心角60度、円周角はその半分という問題です。
(2)△ABPと△RBOが相似と気づけば相似比は4:ルート5、そこから3辺の長さが分かります。PRは単なる引き算ですね。
(3)またもやヘロンの公式かと思いましたが先ほどの大問2(4)と同様、長方形APBQ(面積32)から左下(面積6)、右上(面積5)、右(面積8)の3つの三角形の面積を引きます。
で、ARとの距離(つまり最短距離)は、ARを底辺をした時の三角形の高さでした。
(4)外接円の半径を求めるためには正弦定理が、そしてsinの値を知るためには余弦定理が必要というラスボス感のある問題、保護者世代では中学校で習わなかったので子供にこの問題の解き方を聞かれても答えられません。
とりあえず三角形の角のうちどこでもいいのですが何となく簡単そうな角QOBあたりをXとでもしておき、余弦定理でcosX=3/5とわかれば、sinX=4/5なので正弦定理で2R=5です。
大問4 何となくプログラミング言語のような問題ですが2024年度(令和6年度)の問題同様等差数列と等比数列に絡めてきます。
プログラムではなく関数とかメソッドというのが正しいですが。
A: x + n
T: x * n
P: x ^ n
(1) 代入するだけ
(2) 処理順としてはTAPの順ですが、関数は内側から処理するのでPATの順に並んでいること、当然引数もその順に234の順に並んでいるものとなります。
(3) 完全に2次関数の問題です。
(2x) ^ 2 = (x + 2) ^ 2 という2次方程式を解くだけです。
(4) 等差数列が出てきましたが、そんなの知らなくても単なる3の倍数です。
(5) こちらは等比数列ですが、まあ地道に3をかけていくと
3^6 = 729 まだ3桁
3^7 = 2187 ここでやっと4桁、これを3で割るだけ。
以上です。こうやって見ていくと大問1(8)と大問3(4)は保護者世代でも難しいのではないかという感想を持ちました。